Les modèles numériques de terrain (MNT) comme celui proposé par Visual DEM France sont généralement constitués d'un quadrillage d'altitude. Ceci est très pratique pour passer à une représentation en 3D. Il suffit de transformer chaque case du modèles en deux triangles et à injecter l'ensemble dans un moteur 3D. Comme moteur, je prendre VRML pour la suite de cet article. Considérons maintenant un morceau de terrain entre Belledones et Grandes Rousses. Ce morceau fait 20x20 km soit 400 km². A raison d'un point tout les 75 m, nous avons 71 500 points (ou 130 000 triangles) :
Sur mon PC (Celeron 375 sans accélération
3D), ça rame un peu (1 image/s) mais sans plus. Par contre, si on
rajoute une texture par dessus, ça commence à être
plus dur:
(Note : comme la texture fait 2,5 Mo et est commune à
tous les exemples, je vous invite à la télécharger,
ainsi que les fichiers VRML, sur votre PC et à les visualiser
en local).
Maintenant, avec ma texture de 2000x2000 points (10 m de résolution au sol), il est difficile de naviguer (1 image toutes les 3 secondes).
On peut toutefois remarquer qu'avec ce procédé d'échantillonnage à pas constant, dans les zones plates, on pourrait utilement remplacer un grand nombre de petits triangles par un seul grand triangle qui les engloberait. Ceci ne modifierait en rien le paysage tout en simplifiant le calcul de la scène en 3D. Nous obtenons alors un réseau irrégulier de triangle (ou Irregular Triangular Network en anglais). L'image suivante présente le résultat sur le sud est de la Chartreuse :
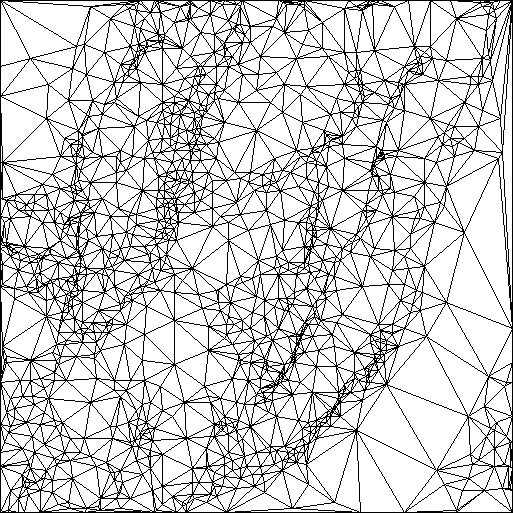
Réseau irrégulier de triangles pour modéliser
le terrain du sud est de la Chartreuse (19x19 km)
Nous observons en bas à droite de grands triangles correspondant à la vallée de l'Isère. Au contraire, les zones avec de nombreux petits triangles sont associées aux falaises.
Il reste à disposer d'un algorithme pour déterminer ce réseau.
Partie mathématique
Delaunay a créé un algorithme qui à partir d'un ensemble de points établit un réseau de triangles les plus compacts possibles, c'est à dire en évitant de former des triangles allongés. Cet algorithme est itératif. On commence par un réseau minimum puis on ajoute un par un les nouveaux points du réseau et on recalcule à chaque fois le réseau de triangles correspondant. Le choix des points n'est pas du ressort de l'algorithme mais doit provenir du problème à résoudre.
Partie géographique
On débute en prenant les quatre angles de la zone (rectangulaire) étudiée comme points initiaux du réseau. A ces points, on affecte les altitudes correspondantes dans le MNT :
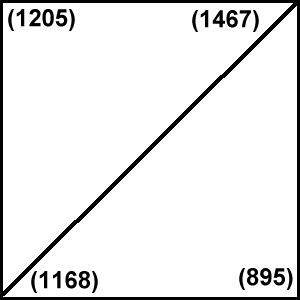
Réseau initial (entre parenthèses, les altitudes des
points)
Un fois découpé en deux, nous avons deux triangles en trois dimensions qui constituent une première approximation du terrain. Dans le cadre de cette approximation, nous recherchons, pour l'ensemble du MNT, le point où l'approximation est la plus mauvaise. Ce point constitue alors un nouveau sommet qui est fourni à l'algorithme de Delaunay pour calculer le nouveau réseau de triangles :
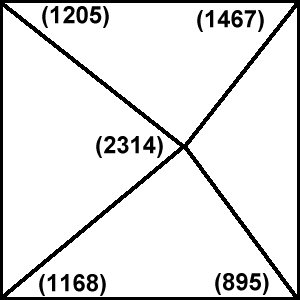
Ensuite, on répète la même opération en ajoutant un par un à chaque fois le point où l'erreur est maximale. Et on s'arrête lorsque l'erreur maximale atteint un niveau acceptable.
Voici le résultat pour le paysage de départ avec une tolérance de 25 m :
Il y une légère perte de qualité
par rapport au paysage de départ. Par contre, nous n'avons plus
que 13 652 points, soit un gain d'un facteur 4. Et ça se ressent
sur l'animation qui est plus fluide (3 images/s).
Rajoutons la texture :
L'animation ralentit (1 image/s) mais reste plus rapide. Et une fois la texture appliquée, il est bien difficile de voir la différence avec le paysage d'origine. D'ailleurs, toujours en présence de la texture, on peut augmenter la tolérance sans voir de différence significative. Voici pour une erreur de 50 m :
Le nombre de sommet a de nouveau baissé et l'animation est encore plus fluide. On peut même pousser à 100 m d'erreur :
De loin ça va. Par contre, il ne faut pas se promener trop près du relief qui apparaît un peu pyramidal.
Un petit tableau pour résumer les gains :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Les gains sont très importants alors que j'ai pris
une zone fortement montagneuse. Du côté de Poitiers, j'obtiens
un gain de 225 avec une tolérance de 25 m.
Pour terminer, j'ai programmé tout ça sous Kylix et Delphi6.
J'ai commencé par récupérer un composant
calculant la triangulation de Delaunay :
le composant : delaunay.zip
(8 ko)
un projet exemple : delproj.zip
(10 ko)
le projet compilé : delexe.zip
(148 ko)
Ce code, qui fonctionne au moins à partir de Delphi
3, provient d'un programmeur tchèque inconnu et dont la page web
a disparue.
J'ai moi même fait une version CLX du composant
: qdelaunay.zip (7 ko).
Puis j'ai créé un projet exemple qui, à
partir d'un fichier texte d'altitudes issu de VistaPro, génère
un réseau de triangle et l'enregistre au format VRML.
Le projet : tin.zip (5 ko).
Le projet utilise la CLX et fonctionne sous Kylix et
Delphi6. Néanmoins, il doit être facilement adaptable à
la VCL et aux anciennes versions de Delphi.